题目有一个很强的提示是“无论怎么走都要能判断出来”,这启示我们可能有很多道路的长度都是相同的。
然后,我们可以这么设计:
当 $i$ 固定时,所有 $a_{i,j}$ 到 $a_{i+1,j}$ 的路的长度均相同。
当 $j$ 固定时,所有 $a_{i,j}$ 到 $a_{i,j+1}$ 的路的长度均相同。
这样,就避免了在不同行中折返走(列同理)的情况。
长这样:
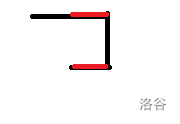
红色是折返走的地方,虽然在不同行但效果一样,如果我们把他们的路径长度赋为相同的权值就可以异或掉了。
通过这个折返走我们可以发现行/列是可以分开考虑的,再由异或想到我们可以用前 $5$ 个二进制位表示行,后 $5$ 个来表示列,所以我们就先对行单独进行分析。
问题就可以被简化成一个一维的图($1$ 列 $n$ 行),你需要对这些路赋值,需要能判断出走到哪儿了。
我们尝试对 $a_{i,1}$ 赋值为 $i$ (注意,是格子,不是路径长度!$a_{i,1}$ 是假设我们已经把它拍扁成一维了),再让 $a_{i,1}$ 到 $a_{i+1,1}$ 的路径的长度赋值为 $i \oplus (i-1)$ ($\oplus$表示异或)。
假设我们当前在的格子的权值为 $t$,询问给你的路径异或值为 $x$,那么你最后到达的格子的权值就是 $t \oplus x$。由于所有格子的权值都唯一,你就可以做到唯一确定了。
到了这里,你得到了一个路径总长度约为 $1.3e5$ 的做法。
优化一:
你看着这个 $i \oplus (i-1)$ 写成二进制后很不舒服,每条路径的长度都有很多个 $1$。然后你想精简它,虽然题目说了长度必须是正整数不能为 $0$,所以最好就让这个长度在二进制下只有一个 $1$。根据你在CSP2019的经验,你想到了格雷码这个东西,编码中相邻的两个数在二进制下恰好相差一位!
这边改改那边改改,你得到了一个总长度约为 $8e4$ 的做法。很遗憾还是过不去
优化二:
再一次观察每条路径的长度。突然发现,路径长度出现的频率是不同的。比如,$2^0$ 出现的频率是最大的,$2^1$ 次之,到 $2^4$ 都是大幅减小,但到了 $2^5$ 又变得和 $2^0$ 一样多了。
探究出现的原因,发现是行&列位数分配不当的原因,原来的方案是对于所有的列的路径长度就要直接乘上 $2^5$。
但这个 $2^4$啊,长度很小,但频率却非常小,感觉上就没有被充分利用。
所以我们考虑用第$0,2,4,6,8$ 位维护行,$1,3,5,7,9$ 位维护列,就可以做到$4.7e4$ 的总长度了。
Code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
| int gc[114514];
int rgc[114514];
inline int GET(int x){
return gc[x];
}
inline void prep(){
gc[0]=0;
for(int i=0;i<6;++i){
int csz=1<<i;
for(int j=0;j<csz;++j){
gc[csz*2-j-1]=csz+gc[j];
}
}
for(int i=0;i<=32;++i)rgc[gc[i]]=i;
}
inline int HANG(int x){
int rt=0;
for(int i=0,j=0;i<5;j+=2,++i){
if(x&(1<<i)){
rt+=(1<<j);
}
}
return rt;
}
inline int LIE(int x){
int rt=0;
for(int i=0,j=1;i<5;j+=2,++i){
if(x&(1<<i)){
rt+=(1<<j);
}
}
return rt;
}
inline int RHANG(int x){
int rt=0;
for(int i=0,j=0;i<5;j+=2,++i){
if(x&(1<<j)){
rt+=(1<<i);
}
}
return rt;
}
inline int RLIE(int x){
int rt=0;
for(int i=0,j=1;i<5;j+=2,++i){
if(x&(1<<j)){
rt+=(1<<i);
}
}
return rt;
}
int k;
inline void solve(){
int n;cin>>n>>k;
fflush(stdin);
for(int i=1;i<=n;++i){
for(int j=1;j<n;++j){
cout<<LIE(GET(j)^GET(j-1))<<' ';
fflush(stdout);
}
cout<<endl;fflush(stdout);
}
for(int i=1;i<n;++i){
for(int j=1;j<=n;++j){
cout<<HANG(GET(i)^GET(i-1))<<' ';
fflush(stdout);
}
cout<<endl;fflush(stdout);
}
fflush(stdin);
int curh=0,curl=0;
for(;k--;){
int x;cin>>x;fflush(stdin);
int l=RLIE(x),h=RHANG(x);
curh^=h,curl^=l;
cout<<rgc[curh]+1<<' '<<rgc[curl]+1<<endl;
fflush(stdout);
}
}
int main(){
prep();
int T=1;
for(;T--;)solve();
return (0-0);
}
|
